Quadrants, neighbourhoods and clusters
Traditionally, small cities were divided in quadrants (quartiers) often by virtue of the two perpendicular main streets that intersected at the center, not by intent to subdivide it. The size of towns during the foot and horse transport eras was typically from 60 to 80 ha (160 to 200 ac) and the quartier, one quarter, would be between 15 to 20 ha (40 to 50 ac). “Quartiers” soon assumed a social dimension (eg labourers quarters) as their size ( about ten to fifteen city blocks) and partly their geographic definition made them a convenient locus for networking, the closely knit neighbourhood.
The Fused Grid is composed of quarters by following the same critical dimension of a comfortable walking distance (especially when loaded or infirm) that governed the size of earlier cities – 400 (1300 feet). This distance is also use by public transit planners to assign bus routes within a district or region (see City District) for the same reason.
The structure of a quadrant There are two basic ways of structuring a quadrant and from these and their combinations several variations have been developed and more are possible. The essential principle is that streets within the quadrant do not traverse it; they either stop or return to the perimeter of it. The second key idea is that all streets are connected with pedestrian/bicycle paths that make the entire quadrant (neighbourhood) easily traversable on foot. The third element of its structure is the neighbourhood open space. This space functions as a passage for the pathways; a crossover point for the paths, which enables continuous walking without crossing streets; a focal point for the neighbourhood; and a recreation and play space.

Quadrant Diagonal - position of open spaces
Transformation from traditional grid to loops
Transformation of conventional cul-de-sacs into a virtual grid
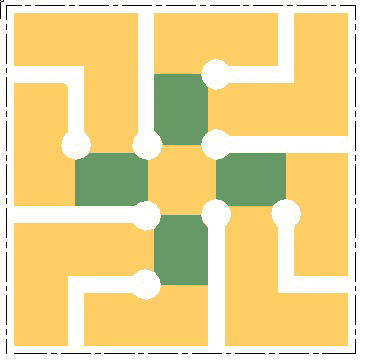
Quadrant Cross - cross-like connecting open spaces
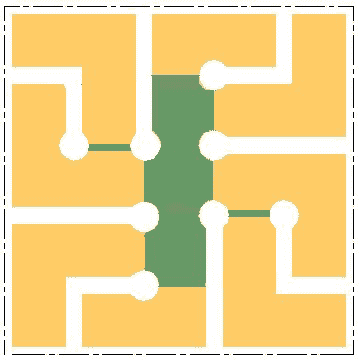
Quadrant Cross
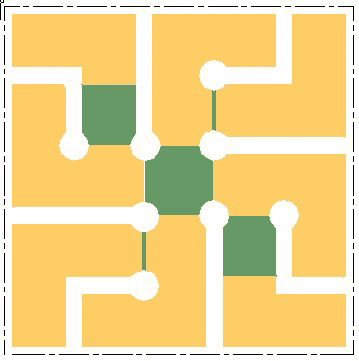
Quadrant Diagonal
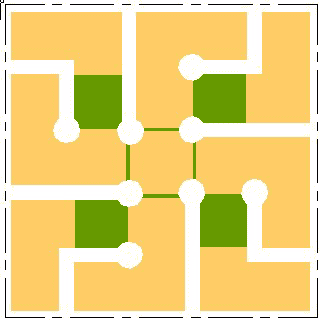
Quadrant Four Square
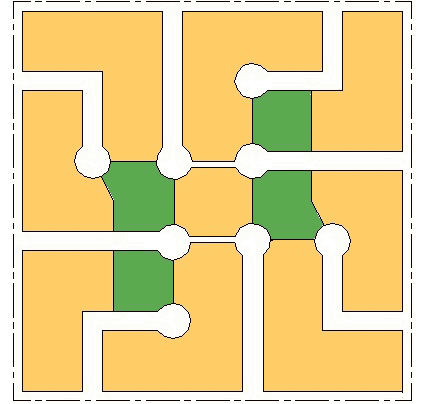
Quadrant Cross
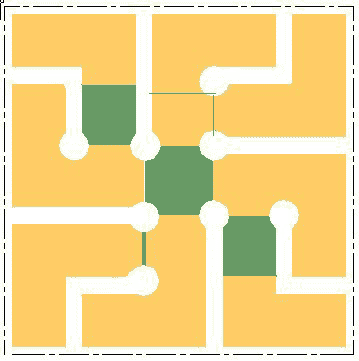
Quadrant Diagonal

Quadrant Four Square